1 2 3 4 5 6 To 100

One way to make it accurate is by adding seven plus and minus signs like so. 1 2 3 4 5 6 7 8 9 100. 500500 is the answer.

devil may cry vergil devil trigger devil survivor 2 the animation characters devil may cry v devil may cry 5 wallpaper 1920x1080 hd derive k e 1 2mv 2 devil may cry 5 dante wallpaper hd derivative of cos 1 e x devil may cry 5 van interior

How To Add Consecutive Integers From 1 To 100 9 Steps

1 2 3 4 5 6 7 8 100 Brainly Co Id

What Does 1 2 3 4 5 6 7 8 9 Up Until 100 Equals To Quora

Berapa Hasil 1 2 3 4 5 6 7 99 100 Tolong Bantu Ya Brainly Co Id

How To Add 1 Through 100 Using Calculus Betterexplained

Problem Solving Made Easy Sum Of 1 2 3 100 Problem 9 Ks3ks4 Youtube

But i have already noticed at a previous time that it is necessary to give to the word sum a more extended meaning.

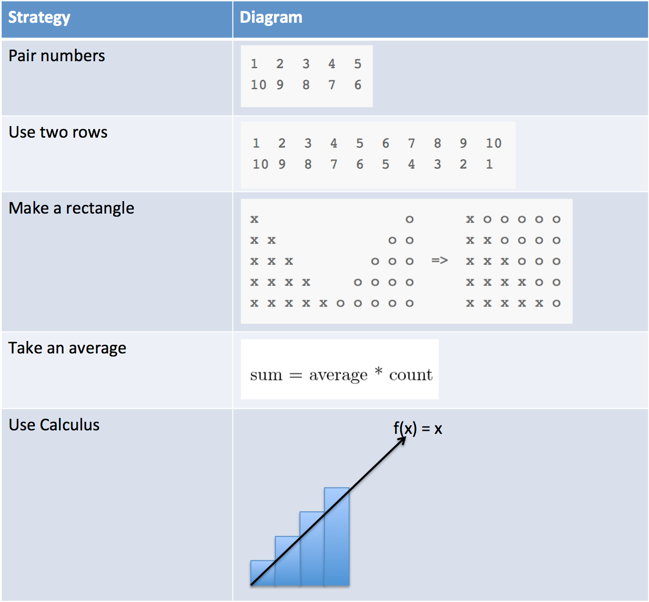
1 2 3 4 5 6 to 100. Let s look at a small set. Shake hands with arithmetic sequences. Since there are 100 of these sums of 101 the total is 100 x 101 10 100. To get the average notice that the numbers are all equally distributed.

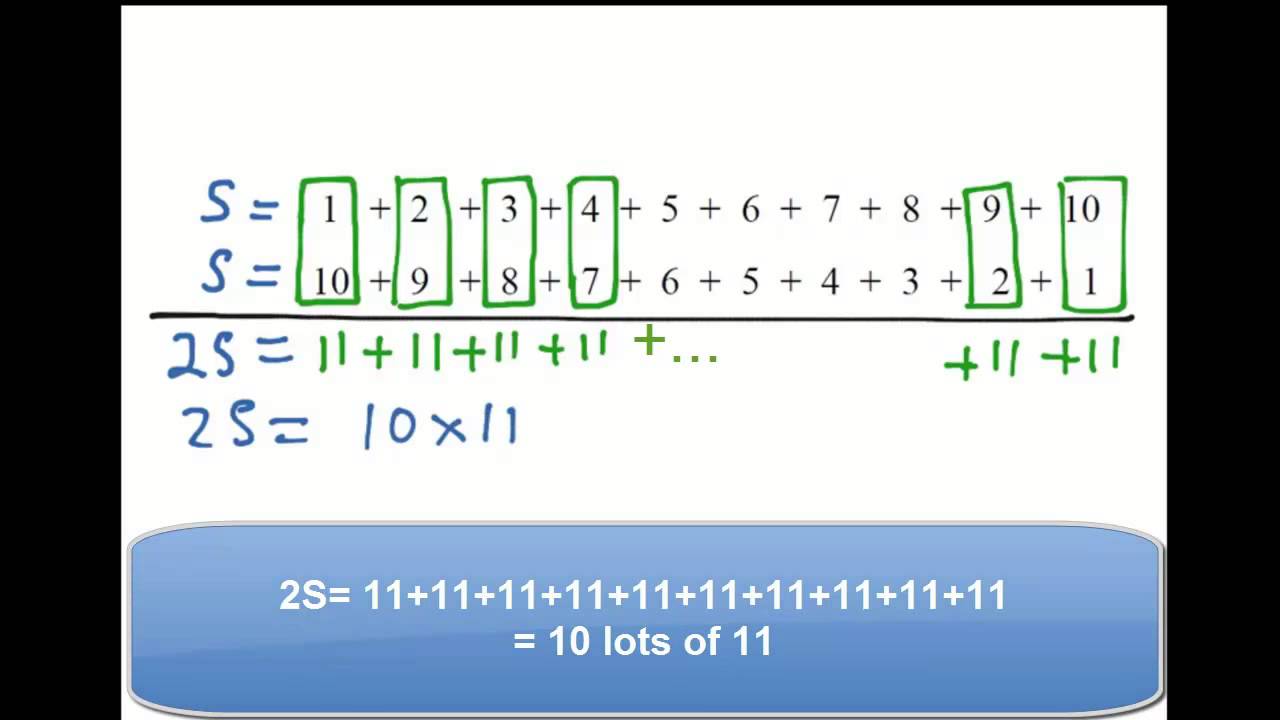
Because this sum 10 100 is twice the sum of the numbers 1 through 100 we have. For by adding 100 terms of this series we get 50 however the sum of 101 terms gives 51 which is quite different from 1 4 and becomes still greater when one increases the number of terms. Thanks to gauss there is a special formula we can use to find the sum of a series. 1000 1001 2 or 500500.

This equation is incomplete. Now for yr 7 or 8 the method is to find a pattern. This equation was. The sequence of numbers 1 2 3 100 is arithmetic and when we are looking for the sum of a sequence we call it a series.

If we have 100 numbers 1 100 then we clearly have 100 items. S is the sum of the series and n is the number of terms in the series in this case 100. It is believed that gauss was the first person who discovered this beautiful method of finding such a sum. The sum of consecutive integers from 1 up to n is n n 1 2 so we use.

For every big number there s a small number on the other end. One easy way to see this is that if you line up the numbers from 1 to say 6 and then the numbers from 6 to 1. So adding the first and last numbers off we get 101 each. The sequence of numbers 1 2 3 4 5 6 7 8 9 has the property that you can insert mathematical operators in between the numbers from 1 to 9 and make the.

1 2 3 4 5 6 78 9 100. So let s figure out the sum. . The partial sums of the series 1 2 3 4 5 6 are 1 3 6 10 15 etc the nth partial sum is given by a simple formula.

Notice that 1 100 is 101 2 99 is 101 3 98 101 in that order.